Clock Mainsprings

When replacing a clock mainspring, the repairman usually finds the closest match in his supplier's catalog to the mainspring being replaced. Frequently this may be incorrect because it may be too strong or too weak, or of an incorrect length. The best way to determine the correct mainspring is to build up a database of mainspring data: record the information about the mainspring and the clock for each clock that you overhaul. By the time you have fifty clocks recorded, you will develop an idea of what strength of spring is suitable for what type of clock, when a spring is too powerful and should be replaced with a weaker one, or vice-versa. In general, the strength of a spring is proportional to the cube of the thickness: if you double (2) the thickness, the spring is eight (=2x2x2) times stronger. The width is directly proportional to the strength: if you double the width, you double the strength. This assumes, of course, that the steel and the temper are the same in both springs being compared, which cannot reliably be ascertained, but we can at least use this information as a guideline at the bench. Below is a chart that you could use, showing the relationship between thickness and strength of two otherwise identical springs. When the relationship is expressed in percentages, it could be applied to any situation.

This is the formula to use to determine the correct mainspring length:

where L is length, T is thickness, R_a is the arbor radius (half the diameter of the arbor), and R_b is the barrel radius (half the inner diameter of the barrel). This formula could be entered into a computer spreadsheet as:

or:

Below is also a spreadsheet that you could download and use for yourself. If you enter the dimensions, it would give you the answer. The diameter of the barrel and the diameter of the arbor are measured in millimetres and should include an allowance for the barrel hook and the arbor hook. The thickness of the spring is measured in inches because the suppliers do not all list the thickness in millimetres. This is confusing, but I have had to learn to live with it. Enter the data into cells B1, B2, and B3.

The correct mainspring length that you want will appear in cell D8. The number of turns you could get from the fully unwound position to the fully wound position is given in cell F8. This figure is theoretical: in practice, the net turns is one to two turns fewer, depending on the thickness and the condition of the spring. A thin spring may be less than one, as opposed to two for a very thick spring. A poorly finished spring or one in very bad condition may yield as much as a full turn less than an otherwise identical new one: this can be used to diagnose the condition of a spring once you build up your database.

If your mainspring is not of the same length as the theoretically correct mainspring, you could compare the difference in the net turns, shown in cell F10, in order to decide whether to replace the spring. Also below, you will find another chart showing the length and the net turns. I was surprised to find that using a spring that was 50% too long (or 150%) resulted in a loss of net turns of only about 18%! It makes sense therefore to install a mainspring slightly longer (say by 10%) than the correct length you calculated because if the end were ripped off in the future, the next repairman could make a new hole and still have the correct length.

If you wish to install a spring of another thickness, enter the desired thickness in cell D14. You could then compare the new correct length for the spring in cell D18 and the difference in net turns in cell E19. You could also compare the thickness and the strength in cells D16 and D17.

This spreadsheet can also be used for "open" barrels, as if the clock had a closed barrel. In this example, I show a typical American two-spring clock and imagine that it has a barrel 65 mm in diameter. The table shows that it should have a spring 141 inches long! This is much longer than the 96 inch springs we get from our suppliers, but we only lose 1.24 turns because of this. Since these springs are much too strong for most clocks, I considered a new thickness of 0.0165", which is 8% thinner (=92%), and 23% weaker (=77%, a moderate reduction in strength). If we used a 153" spring 0.0165" thick, we could get over three extra turns compared to a 96" spring 0.018" thick (compare cells F9 and D19).

One more point to consider. Suppose you have two identical clocks except that one has a recoil escapement and the other a Graham. The recoil needs much more power because of its inefficiency. Consider making the spring about 50% stronger, or 15% thicker. If you have two identical clocks but one has a long pendulum, it would require more power than the shorter one. Manufacturers make up for variations in quality control and variations in design by making the springs far more powerful than they need to be, which means that clocks wear out sooner than if they had the correct power. Two notorious examples are the typical American two-spring, like the Seth Thomas #89, and the new Russian submarine clock. A clock with the correct spring will fail when the lubricant fails. A very overpowered clock will run long after the lubricant has failed, grinding its way through the dirt, damaging the clock. While you do not want a spring with barely enough power to run the clock because it may fail to run a full week, you should consider one that is only moderately overpowered, say by 30%.

Below are a few examples of how I collect mainspring data. You might consider something similar that suits your needs for building a database of information.

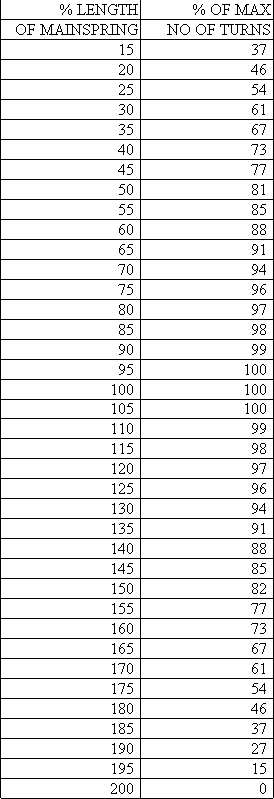
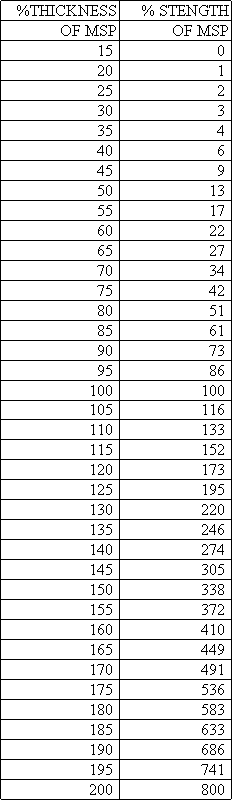
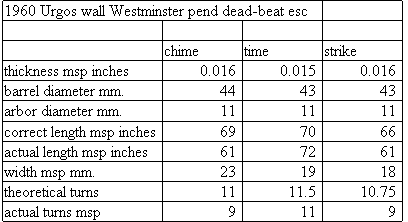
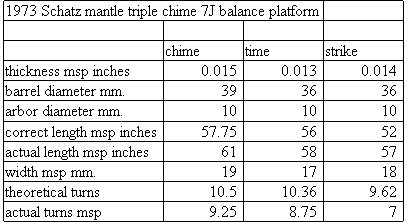
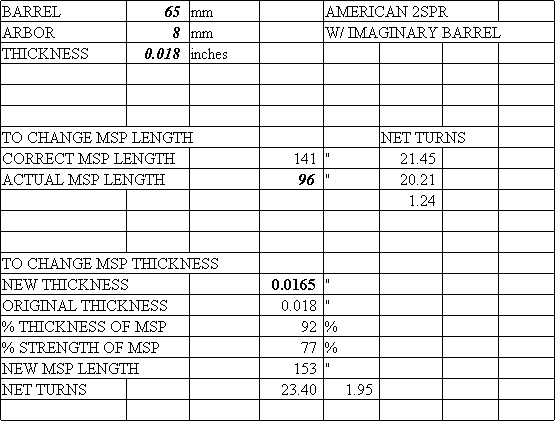
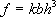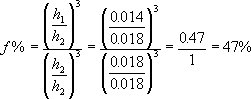Here is the spreadsheet you could use to calculate mainspring lengths. You should be able to download it into your computer and save it. This is a ZIP file and contains an MS Works 4.0 and an Excel 4.0 file (Win95) and looks like the chart below. The numbers in bold are where you enter your data.

Mainsprings for American Clocks
I am interested in finding a way to measure the force exerted by mainsprings, but have been unable to find one accurate enough to yield useful results. I applaud Mr. Boxhorn's effort in the January 1997 issue of the Clockmaker's Newsletter.

While I agree that many of the mainsprings on the market intended for American clocks are excessively powerful, I urge caution in dramatically reducing the applied strength when replacing one. The 0.014" spring may work well when new, but in a few years it may have problems as it loses some strength. There are many reasons why caution should be exercised. I will only mention three:

1: American clocks, such as the Seth Thomas #89 movement, have pivots in the upper end of the train, (fourth wheel, escape wheel, warning wheel, governor, and pallets), that can be as much as 50% thicker (or of even greater diameter) than pivots in most foreign clocks. Exceptions include large, higher grade European grandfather clocks, French Morbier clocks, and oriental reproductions of American clock movements. Bigger pivots result in more friction because a greater circumference of pivots passes by for every turn the gear makes, and this higher level of friction is exacerbated when the lubricant gets older and thickens and has a dragging effect on the turning pivot. Further, the binding effect caused by a floating particle contaminating the bushing lubricant is much greater as the particle becomes jammed between the pivot and the bushing wall in the worn portion of the bushing as the pivot continues to turn.

2: The typical American clock escapement is a strip recoil escapement, which makes no pretense of being efficient. More power needs to be applied to the pallets to make up for this inefficiency: I would suggest at least 50% more than for a deadbeat escapement. I came to this conclusion by comparing a typical early 19th C. British grandfather clock with a recoil escapement and a typical early 20th C. German grandfather clock with a deadbeat escapement and cable-driven weights. The British clock needs a much heavier weight for the time-train. The efficiency of the escapement depends on the angles of the pallets' impulse faces relative to the respective tangents off the circle made by the tips of the escape wheel teeth. These angles vary widely, and therefore so do the efficiencies of the escapements. Some excess power is necessary to overcome this.

3: Different pendulums have different power requirements. A short and light pendulum with a thinner suspension spring needs less power than a longer and heavier pendulum with a thick suspension spring. A heavier Seth Thomas 124 pendulum may stop when hung on an Ingraham high-beat clock that was intended to have a light pendulum. There is argument about how heavy a pendulum should be and what effect this has on accuracy. I expect this argument may never be resolved because these variables cannot be quantified. However, we can safely say that a heavier pendulum usually needs a thicker suspension spring to prevent wobble and more power from the escapement to keep it going.

I feel that point #2 above is the most critical, because so much power is lost in even the best-designed escapements.

Since there is so much unknown about the power requirement about a particular clock, manufacturers wisely choose to err in favor of some excess power to make up for variations in manufacture and for differences between movements. Repairmen should do the same.

Since there are some repairmen, however, who are intent upon using weaker mainsprings, the following information may help. Mr. Dan Henderson, a Senior Manufacturing Technology Engineer at 3M, shared with me a formula for springs. All other factors being equal, the strength of the spring is proportional to its width: in other words, if we double the width, we double the strength. Similarly, the strength is proportional to the cube (to the power of 3) of the thickness: if we double the thickness, the spring is eight times stronger (2x2x2=8).

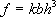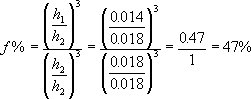where f is force (or strength), b is the base (or width of the mainspring), and h is the height (or thickness of the mainspring). This means that the 0.014 inch mainspring has 47% of the strength of the 0.018 spring. I would be very careful in replacing a mainspring with one that is less than half as strong as the former.

K in the above formula is a constant, or a number. It reflects other factors that affect the strength of the spring. These include the shape of the spring, the temper and composition of the metal, variations in thickness along the length of the spring, whether the spring is new or several years old, to name a few. Since it is very unlikely that two springs will be of the same temper, etc, this formula does not provide a precise measure of strength: it can, however, provide a guideline for a clockmaker comparing two springs that appear to be similar, such as two new mainsprings from the same manufacturer, but of different thicknesses.

Timesavers is now selling a new mainspring for American clocks, part number 18790. It is 3/4" wide, 0.0165" thick, and 96" long. By the above formula, we can approximate it to have 77% of the strength of a similar 0.018" thick spring. If you believe that the mainspring in your American clock is too strong, I recommend that you try this mainspring. I have used it several times. I feel that a more moderate reduction in power would be more prudent.

Mainsprings in American Clocks

Clock Repair Main Page
Escapements in Motion
Links Page